
| Month |
January
|
February
|
March
|
April
|
May
|
June
|
|---|---|---|---|---|---|---|
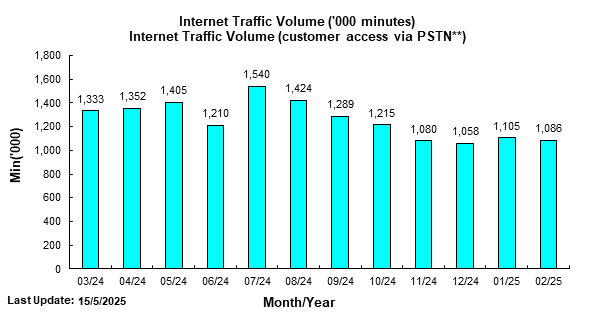
| 2025 | 1,105 | 1,086 | 1,209 | 1,117 | 1,142 | 1,177 |
| 2024 | 1,438 | 1,213 | 1,333 | 1,352 | 1,405 | 1,210 |
| 2023 | 1,909 | 2,157 | 2,286 | 1,560 | 1,608 | 1,684 |
| 2022 | 4,715 | 4,288 | 5,999 | 4,258 | 3,831 | 3,815 |
| 2021 | 8,019 | 5,508 | 7,947 | 5,983 | 5,184 | 5,163 |
| 2020 | 9,073 | 11,908 | 13,502 | 11,896 | 10,232 | 9,836 |
| 2019 | 12,487 | 8,783 | 12,312 | 11,871 | 12,041 | 10,997 |
| 2018 | 14,937 | 11,244 | 14,863 | 13,683 | 15,053 | 14,171 |
| 2017 | 15,570 | 16,319 | 19,674 | 18,936 | 17,333 | 17,851 |
| 2016 | 17,216 | 14,650 | 19,841 | 18,770 | 19,463 | 19,872 |
| 2015 | 20,212 | 15,806 | 24,132 | 21,289 | 20,425 | 22,178 |
| 2014 | 18,402 | 17,998 | 21,338 | 22,112 | 21,091 | 21,185 |
| Month | July | August | September | October | November | December |
|---|---|---|---|---|---|---|
| 2025 | 1,268 | 1,200 | 1,321 | - | - | - |
| 2024 | 1,540 | 1,424 | 1,289 | 1,215 | 1,080 | 1,058 |
| 2023 | 1,779 | 1,852 | 1,594 | 1,460 | 1,399 | 1,288 |
| 2022 | 3,632 | 3,816 | 2,847 | 2,424 | 2,473 | 1,860 |
| 2021 | 4,700 | 5,138 | 4,388 | 3,764 | 3,924 | 3,181 |
| 2020 | 9,779 | 10,160 | 9,064 | 7,882 | 8,061 | 7,458 |
| 2019 | 11,640 | 11,619 | 11,073 | 10,401 | 10,442 | 8,732 |
| 2018 | 14,238 | 14,399 | 13,299 | 13,022 | 13,293 | 10,506 |
| 2017 | 16,470 | 17,1021 | 15,959 | 13,801 | 15,444 | 12,303 |
| 2016 | 18,552 | 19,613 | 17,659 | 15,930 | 17,947 | 15,064 |
| 2015 | 22,160 | 20,488 | 20,271 | 18,085 | 18,936 | 16,233 |
| 2014 | 22,528 | 20,767 | 22,503 | 20,774 | 21,090 | 18,248 |
**Not including customers access via leased circuits and broadband services.
Note 1: The figure has been revised to reflect the adjustments filed by Internet Service Providers